Did you know that the ratio of the circumference and the diameter of a circle known as Pi (a value of 3.141592657932…) was first calculated by Hindus?
The value of pi is being used in India from ancient times. It gives us an insight about how evolved our past was.
Indians were the first to observe that the perimeter (circumference) of a circle increases in proportion to its diameter. Therefore, our ancestors established the relation- perimeter / diameter = constant. Never did they know that this constant will be known as Pi!
Since the Indus Valley script is not completely deciphered, it will be incorrect form my side, to claim that Π was known to Indians in 3000 BC. But they did know the value of Pi by the time Rigveda was written! The Vedangas and Sulabasutras also mention the value of Π. The oldest of them, the Baudhayayana Sulabasutra claims that the perimeter of a pit is 3 times its diameter- therefore approximating the value of Π at 3. Many other texts, including the Mahabharata (Bhishmaparva, XII: 44) and many Puranas approximate Π at the value of 3.
Later, many other Sulabasutras mention the value of Π to be 18 * (3 – 2 √2) = 3.088. The Manava Sulabasutra approximates the value of Π to be 28/5= 3.125. The ancient Jaina school of mathematics preferred the approximation Π = √10. This value of Π has been used not only by Jainas, but also by the greats like Varahamihira, Brahmagupta and Sridhara.
Science and spirituality both moved together in this land.
The Sanskrit text, by the famous Hindu mathematician, Baudhayana in his Baudhayana Sulbha Sutra of the 6th century BC mentions this ratio as approximately equal to 3.
The Hindu mathematician, Aryabhatta, in 499 AD worked out the value of Pi to the fourth decimal place as [3x (177/1250) = 3.1416]. In 825 AD one Arab mathematician Mohammad Ibna Musa said: This value has been given by the Hindus [Indians] (62832/20,000 = 3.1416).
haturadhikaM shatamaShTaguNaM dvAShaShTistathA sahasrANAm AyutadvayaviShkambhasyAsanno vr^ttapariNahaH.Even more important however is the word "Asanna" - approximate, indicating an awareness that even this is an approximation.
[gaNita pAda, 10] Aryabhatiyam (499 CE)
“Add 4 to 100, multiply by 8 and add to 62,000. This is approximately the circumference of a circle whose diameter is 20,000.”
i.e.
correct to four places.
Aryabhatta called it an approximate (asanna) value to mean that not only is this an approximation but that the value is incommensurable (or irrational).
It is quite a sophisticated insight, because the irrationality of pi was proved in Europe only in 1761 by Lambert!
Katapayadi Encryption
gopiibhaagya madhuvraataH shruMgashodadhi saMdhigaH .This shloka, a hymn to Lord Krishna or Shiva, gives the value of pi upto 31 decimal places.
khalajiivitakhaataava galahaalaa rasaMdharaH
Katapayadi system is used to encode numbers in many shlokas
ga - 3 pii - 1 bhaa - 4 gya - 1 ma - 5 dhu - 9 ra - 2 ta -6 shru - 5 ga - 3 sho - 5 da - 8 dhi - 9 sa - 7 dha - 9 ga - 3 kha - 2 la - 3 jii - 8 vi - 4 ta - 6 kha - 2 ta - 6 va - 4 ga - 3 la - 3 ra - 2 sa - 7 dha - 9 ra – 2
pi = 3.1415926535897932384626433832792
So we needed pi upto 31 decimal places! What is more amazing is that we knew encryption! Science and spirituality both were important and both moved together.
Madhava of Sangamagrama
Madhava's work on the value of π is cited in the Mahajyānayana prakāra ("Methods for the great sines"). While some scholars such as Sarma feel that this book may have been composed by Madhava himself, it is more likely the work of a 16th-century successor.This text attributes most of the expansions to Madhava, and gives the following infinite series expansion of π, now known as the Madhava-Leibniz series.
which he obtained from the power series expansion of the arc-tangent function. However, what is most impressive is that he also gave a correction term, Rn, for the error after computing the sum up to n terms. Madhava gave three forms of Rn which improved the approximation, namely
- Rn = 1/(4n), or
- Rn = n/ (4n2 + 1), or
- Rn = (n2 + 1) / (4n3 + 5n).
where the third correction leads to highly accurate computations of π.
It is not clear how Madhava might have found these correction terms. The most convincing is that they come as the first three convergents of a continued fraction which can itself be derived from the standard Indian approximation to π namely 62832/20000 (for the original 5th-century computation)
He also gave a more rapidly converging series by transforming the original infinite series of π, obtaining the infinite series
By using the first 21 terms to compute an approximation of π, he obtains a value correct to 11 decimal places (3.14159265359). The value of 3.1415926535898, correct to 13 decimals, is sometimes attributed to Madhava,but may be due to one of his followers. These were the most accurate approximations of π given since the 5th century
The text Sadratnamala, usually considered as prior to Madhava, appears to give the astonishingly accurate value of π =3.14159265358979324 (correct to 17 decimal places). Based on this, R. Gupta has argued that this text may also have been composed by Madhava.
.jpg)
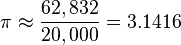


No comments:
Post a Comment